一天，一只蜗牛爬上一棵大树，最后爬到一根树枝的末端。从他从未去过的这么高的地方往下看是多么不同的感觉啊！但是，由于爬了很长时间，他很累，睡着了。当他醒来时发生了一件难以置信的事情——他发现自己躺在一片草地上，原来躺在他背上的房子不见了！他立刻意识到他睡觉时从树枝上掉下来了！他确信他的房子一定还在他睡觉的树枝上。蜗牛又开始爬树了，因为没有房子他就不能生存。
   当到达树的第一个分叉处时，他伤心地发现他记不起以前爬过的路线。为了找到他可爱的房子，蜗牛决定到每一根树枝的末端去。没有房子的保护，走路是危险的，所以他想用最好的方法去寻找那棵树。
   幸运的是，树上住着许多热心的虫子，它们能准确地告诉蜗牛，在它掉下来之前，它是否去过它们的地方。
    现在我们的工作是帮助蜗牛。我们主要关注树的两个部分——树枝的分叉和树枝的末端，我们称之为“关键点”，因为关键事件总是发生在那里，比如选择一条路，得到蠕虫的帮助，到达他正在寻找的房子。
    假设所有蠕虫都生活在关键点，并且相邻两个关键点之间的所有分支的距离都为1。蜗牛现在在树的第一个分叉处。
    我们的目的是通过分析树的结构和蠕虫的位置，找到一条合适的路线，让他尽快找到自己的房子。路线上唯一的限制是，他必须从一个岔口走下去，直到他到达从这个岔口长出来的所有末端。
    房子可能以同样的概率留在任何分支的末端。我们关注的是数学上对蜗牛在到达房子之前所要达到的距离的期望。我们希望价值尽可能小。
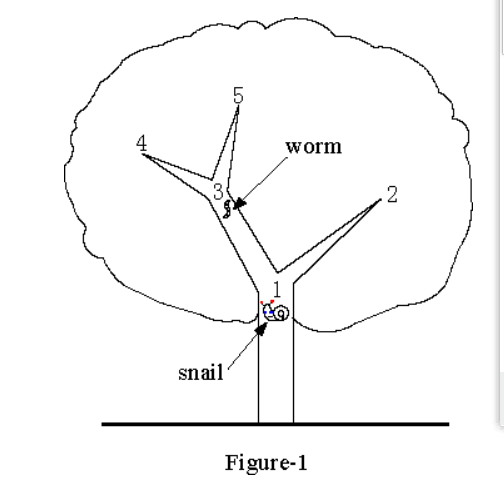
    如图1所示，蜗牛在关键点1，它的房子在2、4和5之间的某个点上。蠕虫生活在第三点，谁能告诉蜗牛他的房子是否在第四点和第五点之一。因此，蜗牛可以选择两种策略。他可以先到第二点。如果他在那里找不到房子，他应该回到第1点，然后在第3点到达第4点（或第5点）。如果仍然没有，他必须返回点3，然后去点5（或4），在那里他无疑会找到他的房子。在这一选择中，蜗牛的距离分别为1、4、6，与房屋位于第2、4（或5）、5（或4）点的情况相对应。所以期望值是（1+4+6）/3=11/3。显然，这种策略没有充分利用来自蠕虫的信息。如果蜗牛走到第3点，首先从蠕虫那里得到有用的信息，然后选择回到第1点，然后再回到第2点，或者走到第4点或第5点，抓住机会，它所覆盖的距离将是2、3、4，与房子的不同位置相对应。在这种策略中，数学期望值将是（2+3+4）/3=3，这正是蜗牛搜索树的路线。

输入包含多组测试数据。每组以一行开头，包含一个不超过1000的整数n，表示树中关键点的数目。然后按照N行描述N个关键点。为了方便起见，我们对所有关键点进行编号，编号为1的关键点始终是树的第一个分叉。其他数字可能是树中除第一个分叉以外的任何关键点。这些n行中的第i行用数字i描述关键点。每行由一个整数和一个大写字母“y”或“n”组成，用一个空格隔开，表示上一个关键点的编号以及是否有蠕虫存在（“y”表示生命，“n”表示没有）。前一个关键点是指该关键点与编号为1的关键点之间最短路径上的相邻关键点。在上图中，点2或3的上一个关键点是点1，而点4或5的上一个关键点是点3。对于关键点1，此整数为-1，表示它没有以前的关键点。你可以假设一个叉子最多有八个分支。样本输入中的第一组描述了上述说明。
n=0的测试用例表示输入结束，不应进行处理。

每一组输入数据输出一行。该行包含一个浮点数，小数点后正好有四位数，即数学期望值。
n=0的测试用例表示输入结束，不应进行处理。

5
-1 N
1 N
1 Y
3 N
3 N
10
-1 N
1 Y
1 N
2 N
2 N
2 N
3 N
3 Y
8 N
8 N
6
-1 N
1 N
1 Y
1 N
3 N
3 N
0

3.0000
5.0000
3.5000

树形DP